Podvodné ruletové strategie a proč nefungují
- Ruletová strategie Martingale
- Fibonacciho ruletová strategie
- D‘Alembertova ruletová strategie
- Laboucherova ruletová strategie
Ruleta je jednou z nejoblíbenějších kasinových her na světě. Mimo jiné to také znamená, že se o této hře nachází na internetu obrovské množství informací. Některé tyto informace jsou použitelné a líčí věci tak, jak se skutečně mají. Existuje však spousta webových stránek, které se snaží lidi oklamat a přimět je k hraní rulety pod záštitou toho, že budou dlouhodobě vyhrávat peníze.
To ale bohužel není možné. Správně fungující ruletu není možné dlouhodobě porážet a neustále obírat kasino o peníze. Nemožnost porazit ruletu je hluboce zakořeněná v matematických a statistických základech této hry. Podrobněji se tomuto tématu budu věnovat později.
Pokud chcete zjistit, proč je nemožné porazit ruletu a proč často prezentované ruletové strategie, které slibují zaručené výhry, prostě nefungují, čtěte dál. Rád bych vám vysvětlil, kterým strategiím se vyhnout a proč, abyste se nenechali zlákat zavádějícími informacemi, kterých je plný internet.
Strategie popsané v tomto článku jsou dle mého názoru podvodné, protože často slibují hráčům velké a nepřetržité výhry, což je slib, který není možné dodržet. Existují však strategie, se kterými se dá ruleta hrát velmi efektivně a s maximální šancí na odchod z kasina s výhrou. Můžete si o nich přečíst v mém článku o ruletových strategiích, které fungují.
Proč hráči statisticky přicházejí o peníze při každé sázce na ruletu
Rád bych začal vysvětlením, proč při každé sázce na ruletu přichází hráč v dlouhodobém horizontu o peníze. Jak jsem již zmínil, souvisí to s šancemi na výhru a matematickým pozadím rulety.
Výhernost rulety a výhoda kasina
Každou kasinovou hru můžete charakterizovat tzv. výherností, která statisticky popisuje, kolik procent z každé podané sázky se vrátí hráči. Kdyby měla hra 100% výhernost, šance na výhru nebo prohru by byla stejná. Kasinové hry mají však téměř vždy (až na několik vzácných výjimek) výhernost nižší.
Ruleta není výjimkou. Výhernost evropské rulety je 97,3 %, zatímco výhernost americké rulety je 94,74 %. To znamená, že pokud hráč vsadí 100 $, ze statistického hlediska „vyhraje" na evropské ruletě 97,3 $ a na americké ruletě 94,74 $. Vzhledem k tomu, že tyto výhry jsou nižší než původní sázky, je zcela jasné, že hráč při každé sázce na ruletu statisticky přichází o peníze.
Výhoda kasina je statistická výhoda kasina nad hráči. Spočítáte ji následovně:
Výhoda kasina = 100 % - výhernost
To znamená, že kasino má u evropské rulety 2,7% výhodu a u americké rulety 5,26% výhodu. Proto v dlouhodobém horizontu získá kasino z každé 100$ sázky 2,7 $ v případě evropské rulety nebo 5,26 $ v případě americké rulety.
Další informace o tomto tématu najdete v článku o šancích na výhru v ruletě, který se právě výhernosti a výhodě kasina věnuje.
Abyste tomuto článku porozuměli, musíte přijmout fakt, že neexistuje žádný způsob, jak ruletu porazit, protože při každé provedené sázce statisticky přicházíte o peníze (bez ohledu na to, jaký druh sázky nebo v jaké výši sázku provedete). Přes to prostě nejede vlak.
Nefunkční ruletové strategie
Konečně se dostáváme ke konkrétním ruletovým strategiím, které bývají často prezentovány jako spolehlivý způsob, jak si v kasinu vydělat peníze, ale ve skutečnosti nefungují.
U každé z podvodných ruletových strategií níže uvedu následující:
- Vysvětlení, jak má daná strategie fungovat a jak ji použít.
- Vysvětlení, proč daná strategie ve skutečnosti nefunguje a proč byste přišli o peníze.
- Nasimulované použití strategie, které jasně dokazuje, že jediným možným dlouhodobým výsledkem je ztráta peněz.
Proč jsou tyto strategie tolik oblíbené
Mnoho webových stránek tyto strategie prezentuje jako spolehlivý způsob, jak si na internetu vydělat peníze, protože jejich jediným cílem jsou peníze, které jim plynou z vaší registrace v online kasinu prostřednictvím jejich odkazu. Na tom, že lžou svým čtenářům, jim nezáleží. Následující podvodné strategie mohou být navíc na první pohled velmi lákavé, zvlášť když k nim přidáte zavádějící informace.
To je přesně důvod, proč je tolik webových stránek vychvaluje a proč byste informace o těchto strategiích, které na jiných stránkách najdete, měli brát s rezervou.
Ruletová strategie Martingale
Zdaleka nejoblíbenější podvodnou ruletovou strategií je Martingale (také známá jako systém zdvojnásobování sázek). Do popularity této strategie se zřejmě promítla i skutečnost, že je velmi jednoduchá – může ji použít prakticky kdokoli, aniž by ji musel důkladněji studovat.
Strategie Martingale funguje následovně:
- Prvotní sázkou hráče (například ve výši jednoho dolaru) bude libovolná rovná sázka (červená/černá, sudá/lichá, vysoká/nízká čísla). Sázka na červenou/černou barvu se používá nejčastěji, ale ze statistického hlediska mezi nimi není žádný rozdíl.
- Pokud hráč vyhraje, vrátí se k prvnímu kroku a vsadí opět jeden dolar. Pokud hráč prohraje, sázku zdvojnásobí a ve zdvojnásobování pokračuje, dokud nevyhraje. Poté se vrátí k prvnímu kroku a vsadí zase jeden dolar.
Strategie Martingale funguje cyklicky. Délka jednotlivých cyklů se liší, ale každý z nich by měl skončit buď výhrou jednoho dolaru, nebo prohrou všeho. Nejprve vysvětlím, jak to funguje, když vyhráváte, a o prohrách se budeme bavit následně.
Zde je několik příkladů výherních cyklů strategie Martingale:
- Hráč vsadí 1 $ a vyhraje 2 $. Čistá výhra je 1 $.
- Hráč vsadí 1 $ a prohraje. Poté vsadí 2 $ a vyhraje 4 $. Hráč celkem vsadil 3 $ a vyhrál 4 $. Čistá výhra je 1 $.
- Hráč vsadí 1 $ a prohraje. Následně vsadí 2 $, 4 $, 8 $, 16 $, 32 $, 64 $, 128 $ a 256 $ a všechny tyto sázky prohraje. Potom vsadí 512 $ a vyhraje. Celkově vsadil 1023 $ a vyhrál 1024 $. Čistá výhra je 1 $.
Ve všech těchto případech byl hráč úspěšný, ale jak už vám asi došlo, ten poslední byl oproti prvním dvěma mnohem horší. Prohrál devět sázek v řadě a vyhrál až tu desátou. To znamená, že musel vsadit 512 $, jen aby za celý cyklus vyhrál 1 $. Strmý nárůst výše sázek je u strategie Martingale jedním ze zásadních problémů.
Proč se zdá, že strategie Martingale funguje
Existuje velmi jednoduché logické vysvětlení, proč by strategie Martingale měla fungovat. Pokud budete neustále zdvojnásobovat svou prvotní sázku, ruletová kulička se přece musí dříve či později zastavit na výherním čísle, že ano?
Ano, je to pravda. S počtem pokusů blížícím se nekonečnu se pravděpodobnost neúspěchu blíží nule. To znamená, že kdybyste disponovali neomezenými prostředky a kasino neuplatňovalo žádná omezení, nakonec byste vyhráli a cyklus ukončili čistou výhrou ve výši jednoho dolaru.
Kdybyste tedy měli neomezené prostředky a kasino neuplatňovalo žádná omezení, systém by fungoval. Asi už vám ale došlo, že tyto dvě podmínky nebudou ve skutečném světě nikdy splněny. Podívejme se na tyto problémy podrobněji.
Problém číslo 1: Omezený rozpočet
V reálném světě nemá žádný hráč neomezený rozpočet. To znamená, že pokud hráč dlouhodobě používá strategii Martingale, časem vyčerpá všechny peníze a nebude moct podat další sázku a dokončit výherní cyklus.
Pojďme si to vysvětlit na konkrétním příkladu. Představte si hráče, který má 1 000$ rozpočet, používá strategii Martingale a jako prvotní sázku 1 $. S 1 000 $ si může hráč dovolit podat tuto řadu sázek: 1 $, 2 $, 4 $, 8 $, 16 $, 32 $, 64 $, 128 $ a 256 $. Celkový součet sázek je 511 $, což znamená, že když je všechny prohraje, zbyde mu pouze 489 $ a nebude moct podat další sázku, která by měla být ve výši 512 $.
Pro účely svých výpočtů jsem se ale rozhodl tuto skutečnost ignorovat a výše popsaný případ považovat za selhání. Na druhou stranu ve svých simulacích, ke kterým se brzy dostaneme, jsem simulovaným hráčům při nedostatku peněz dovolil v souladu se strategií Martingale vsadit zbytek rozpočtu a pokračovat.
Mohli byste namítnout, že takový scénář je značně nepravděpodobný, vždyť by hráč musel prohrát devět sázek v řadě. Na první pohled se to může jevit jako téměř nemožné, ale opak je pravdou. Stává se to častěji, než si myslíte.
Pravděpodobnost, že na evropské ruletě prohrajete rovnou sázku devětkrát v řadě, je:
(19/37)^9 = 0,0025 = 0,25 %
Ano, je to malé číslo, ale tato pravděpodobnost znamená, že statisticky hráč při strategii Martingale prohraje devět sázek v řadě jednou za 402 cyklů s tím, že už nebude schopen podat další sázku.
Pokud hráč navýší svůj rozpočet alespoň na 1 023 $, bude mít samozřejmě dostatek peněz na to, aby po prohrání všech předchozích sázek vsadil 512 $, a mohl si tedy dovolit prohrát deset sázek v řadě. V takovém případě nebude moct provést další sázku jen zhruba jednou za 784 cyklů.
Pravděpodobnost prohry jednoho cyklu je tedy s dostatečným rozpočtem velmi nízká. Pokud však chcete vyhrávat peníze dlouhodobě, musíte celý proces mnohotisíckrát opakovat, což znamená, že dříve či později celý rozpočet stejně prohrajete. Simulace strategie Martingale, na které se za chvíli podíváme, to jasně dokazují.
Problém číslo 2: Omezení výše sázek
Strategie Martingale je omezená nejen rozpočtem, ale také výší sázek, které konkrétní kasino přijímá. Maximální a minimální výše sázek se samozřejmě v závislosti na kasinu nebo hře liší, ale obecně je maximální povolená sázka pouze několiksetkrát vyšší než minimální sázka.
Při hraní v online kasinech můžete tato omezení obejít tím, že budete používat několik online rulet s odlišnými velikostmi sázek. Není to příliš praktické, ale dopad omezení výše sázek na účinnost strategie Martingale se sníží.
Maximální výše sázky bude ale vždycky nějak omezená, i když se ji pokusíte obejít použitím většího počtu ruletových stolů. Takže i s neomezeným rozpočtem (což znamená, že by se vás výše zmíněný problém číslo 1 netýkal) byste byli stále omezení maximální povolenou sázkou na ruletu.
Problém číslo 3: Nevíte, kdy přestat
Jak jste si už asi všimli, pravděpodobnost, že prohrajete 9 nebo 10 sázek v řadě v jednom cyklu, je poměrně nízká a prohra stovky takových cyklů v řadě také není příliš pravděpodobná. Kdybyste měli rozpočet, který by vám umožňoval podat deset sázek v řadě po prohrání všech předchozích sázek (od 1023 $ do 2046 $) a chtěli byste vyhrát pouze 100 $, pravděpodobnost, že uspějete, by byla:
(1-(19/37)^10)^100 = 0,88 = 88 %
Pokud by tedy vaším cílem bylo vyhrát 100 $, uspěli byste s 88% pravděpodobností. Ve zbývajících 12 % případů byste prohráli podstatnou část svého rozpočtu a nemohli byste podat další sázku.
Pokud by vaším cílem bylo vyhrát 200 $, měli byste 77,5% šanci na úspěch, u 500$ výhry by to byla 52,8% šance a u 1 000$ výhry už pouze 27,9% šance. Jak vidíte, šance na výhru s vyšší cílovou částkou klesá, což je samozřejmě logické.
Problém číslo 3 spočívá v tom, že strategie Martingale zpočátku obvykle funguje, takže hráči získají příliš velkou sebejistotu a myslí si, že tato strategie bude fungovat pořád. Bohužel tomu tak není. Pokud budou používat strategii Martingale dostatečně dlouho, přijdou nakonec o celý rozpočet.
Kdyby hráči věděli, kdy přestat a odejít z kasina, většina z nich by odešla s výhrou. Žádná ideální doba, kdy přestat hrát, ale neexistuje, protože osudnou sérii proher lze jen těžko předvídat. Navíc neexistuje žádná záruka, že hráč neprohraje všechno už v prvním cyklu.
Simulace strategie Martingale
Nasimuloval jsem pět hráčů, kteří při hraní evropské rulety používali strategii Martingale. O těchto simulacích potřebujete vědět následující:
- Každý hráč začal s 1 000$ rozpočtem a prvotní sázkou ve výši jednoho dolaru.
- Simulace se zastaví buď po 10 000 kolech, nebo po prohře celého rozpočtu.
- Hráči podávali sázky podle strategie Martingale.
- Pokud neměli dostatek peněz na podání další sázky, vsadili celý zbývající rozpočet. Pokud sázku prohráli, hra pro ně skončila. Pokud ji ale vyhráli, pokračovali podle strategie Martingale a v dalším kole vsadili jeden dolar.
- Simulace jsem vytvořil ve vlastním simulačním softwaru, který k určení výsledku kola používá generátor náhodných čísel. To platí i pro všechny ostatní simulace v tomto článku. V ruletě sice generuje náhodná čísla samotné hrací kolo, ale výsledky jsou ze statistického hlediska stejné.
Pojďme se podívat na výsledky:
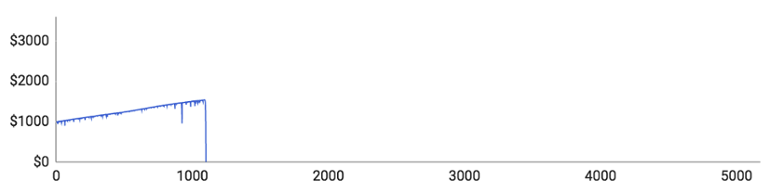
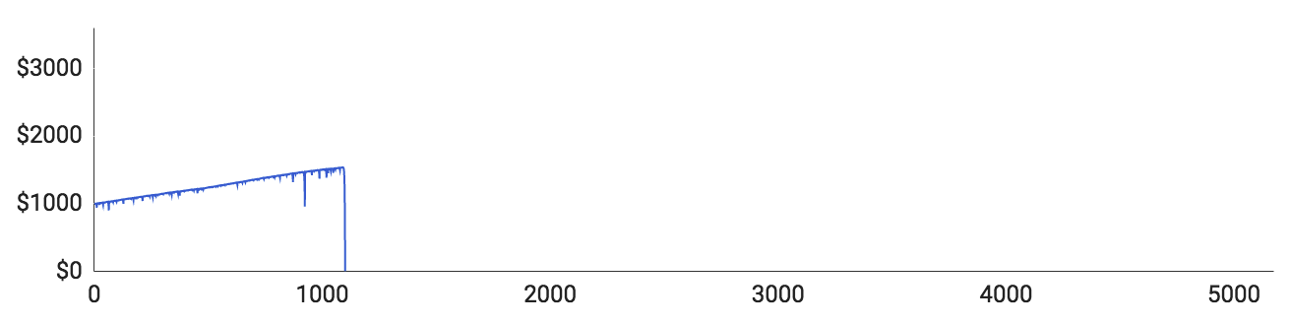
Jak vidíte, všichni hráči prohráli celý rozpočet dřív, než stihli dokončit 10 000 kol. Podívejme se na jednotlivé hráče a na to, jak se jim (ne)dařilo:
- Hráči číslo 1 se ze začátku celkem dařilo. Dokázal svůj rozpočet navýšit o více než 500 $ a narazil jen na jednu delší sérii proher. Potom však prohrál 11 kol v řadě a z 1 540 $ mu nezbylo nic.
- Hráč číslo 2 na tom byl nejhůř ze všech. O všechno přišel po pouhých 51 kolech. To se příliš často nestává, ale aspoň vidíte, že se všechno může zvrtnout hned na začátku.
- Hráč číslo 3 všechno prohrál po 417 kolech. Narazil na jednu delší sérii proher, ze které se vzpamatoval, ale brzy poté ho skolila série 11 proher v řadě.
- Hráč číslo 4 téměř všechno prohrál ve 193. kole, kdy mu zbylo pouhých 70 $. Poté se mu chvíli dařilo a dostal se na 477 $, ale nakonec ho postihla další série proher, při které přišel definitivně o všechno.
- Hráč číslo 5 na tom byl nejlépe ze všech, ale stejně se mu nepodařilo odejít výhrou. Svůj rozpočet dokázal navýšit o 2 308 $. Poté ale prohrál 12 kol v řadě a nezbylo mu nic.
Z těchto simulací vyplývá, že strategie Martingale nemůže dlouhodobě fungovat. Všem hráčům se dařilo pomalu navyšovat svůj rozpočet, ale poté přišla velmi krutá série proher a o všechno přišli. Je patrné, že přestože se dlouhé série proher zdají nepravděpodobné, ve skutečnosti k nim dochází docela běžně.
Fibonacciho ruletová strategie
Fibonacciho ruletová strategie se v mnoha ohledech podobá ruletové strategii Martingale, ale jsou mezi nimi určité rozdíly, a právě na ty se zaměřím.
Nejprve se ale podíváme na to, jak Fibonacciho strategie funguje. Tato strategie vznikla na základě slavné Fibonacciho posloupnosti, která vypadá následovně:
1 – 1 – 2 – 3 – 5 – 8 – 13 – 21 – 34 – 55 – 89 – 144 – 233 – 377 – 610 – 987 – …
Možná jste si všimli (nebo to už víte), že každé číslo v této posloupnosti je součtem dvou předchozích čísel, a přestože to nemusí být na první pohled patrné, stejnou vlastnost sdílí i tato strategie.
Fibonacciho ruletová strategie se používá následovně:
- Hráč začne vsazením částky, která odpovídá prvnímu číslu v posloupnosti.
- Pokaždé když prohraje, přesune se k dalšímu číslu v posloupnosti a vsadí odpovídající částku. Pokaždé když vyhraje, vrátí se o dvě čísla zpět. Pokud se hráč vrátí na začátek posloupnosti, vsází dál částku odpovídající prvnímu číslu, dokud neprohraje a potom pokračuje podle stejných pravidel.
Tato strategie je složitější než strategie Martingale, takže zde je několik příkladů pro snazší pochopení:
- Hráč vsadí 1 $ a vyhraje. Cyklus se tím dokončí a on začne opět od začátku posloupnosti.
- Hráč vsadí 1 $ a prohraje. Potom znovu vsadí 1 $ (je důležité si uvědomit, že tato sázka odpovídá druhému číslu posloupnosti, ne tomu prvnímu) a vyhraje. Nyní by se měl vrátit o dvě čísla zpět, ale protože tímto směrem existuje v posloupnosti pouze jedno číslo (1), vrátí se k němu a opět vsadí 1 $. Pokud vyhraje, dokončí tím cyklus a začne znovu od začátku.
- Hráč vsadí 1 $ a prohraje. Následně vsadí 1 $, 2 $, 3 $, 5 $, 8 $, 13 $, 21 $ a 34 $ a všechny tyto sázky prohraje. Potom vsadí 55 $ a konečně vyhraje. To znamená, že se vrátí k 21$ sázce, od které pokračuje dál.
Výhody a nevýhody Fibonacciho strategie
Mezi Fibonacciho ruletovou strategií a ruletovou strategií Martingale je jeden zásadní rozdíl. Ve strategii Martingale stačí k dokončení vítězného cyklu jedna vyhraná sázka, kdežto u Fibonacciho strategie hráč dokončí výherní cyklus pouze v případě, že se mu podaří vrátit se na začátek posloupnosti a vyhrát sázku, která odpovídá jejímu prvnímu číslu. Jinými slovy, jedna výhra ke zvrácení série proher nestačí.
Proto Fibonacciho strategie potřebuje v porovnání se strategií Martingale větší počet kol k dosažení stejné výhry. Nicméně to také znamená, že Fibonacciho strategie je méně riskantní.
Simulace Fibonacciho strategie
Simulace Fibonacciho strategie jsem provedl skoro stejně jako simulace strategie Martingale. Jediným rozdílem byla použitá strategie.
Pojďme se podívat na výsledky:

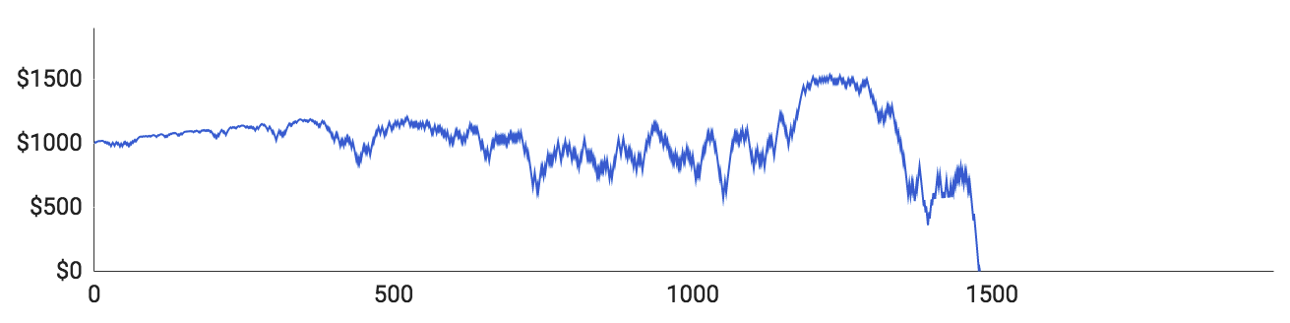
Tyto grafy jsou velmi podobné grafům pro strategii Martingale, ale určité rozdíly se mezi nimi najdou:
- Grafy Fibonacciho strategie rostou mírnějším tempem. To je v souladu s tím, že je Fibonacciho strategie méně riskantní a pro dosažení stejné výhry je potřeba větší množství kol.
- Grafy Fibonacciho strategie jsou kolísavější. U strategie Martingale narůstají jednotlivé rozpočty zhruba stejným tempem, dokud neklesnou na nulu. U Fibonacciho strategie se rozpočty hráčů mění kolísavěji, protože jedna vyhraná sázka nestačí k prolomení série proher.
Nyní se podívejme podrobněji na každého z pěti hráčů:
- Hráč číslo 1 prohrál celý svůj rozpočet jako první. Trvalo to 488 kol a za celou dobu se mu nepodařilo významně navýšit svůj rozpočet. Maximálně se mu podařilo dosáhnout 1 074 $ a nakonec po 11 prohraných kolech skončil na nule.
- Hráč číslo 2 byl úspěšnější. Než prohrál celý rozpočet, trvalo to 2 291 kol a maxima ve výši 1 330 $ dosáhl 27 kol před prohrou celého rozpočtu. Z těch posledních 27 kol vyhrál pouze čtyři a zbylých 23 prohrál, což znamená, že se jeho sázky zvyšovaly a peníze z jeho rozpočtu mizely čím dál tím rychleji.
- Hráč číslo 3 odehrál 4 290 kol, ale jeho rozpočet nikdy nepřesáhl 1 298 $, což je méně než maximum hráče číslo 2. Bylo to kvůli tomu, že v 656. kole téměř všechno prohrál a musel vsadit zbylých 122 $. Dané kolo se mu podařilo vyhrát, poté se mu začalo pomalu dařit, ale nakonec o všechno přišel v sérii proher.
- Hráč číslo 4 všechno prohrál během 1 272 kol a maximálně jeho rozpočet dosahoval 1 175 $. V 1 176. kole musel vsadit zbylých 145 $, a přestože se mu podařilo vyhrát, během následující stovky kol přišel o zbytek.
- Hráči číslo 5 se dařilo nejvíce ze všech. Odehrál neuvěřitelných 7 132 kol a rozpočet se mu podařilo navýšit o 1 269 $. Bohužel na metu 10 000 kol také nedosáhl, protože ho postihla série proher a přišel o všechno.
Celkově vzato je Fibonacciho strategie v mnoha ohledech podobná strategii Martingale. Rozdíl je v tom, že všechno kolísá nahoru a dolů pomaleji. Rozpočet se navyšuje pomaleji, ale zároveň i výše sázek roste pomaleji, když narazíte na sérii proher. V porovnání se strategií Martingale tedy hráči odehráli v průměru více kol a zároveň zaznamenali menší maxima rozpočtu.
D‘Alembertova ruletová strategie
Strategie Martingale i Fibonacciho strategie fungují na základě zvyšování nebo snižování sázek v závislosti na výsledku jednotlivých kol. D‘Alembertův ruletový systém vsázení funguje podobně, ale rozdíly ve výši sázek jsou mnohem menší. Proto je tato strategie mnohem bezpečnější.
D‘Alembertova ruletová strategie také používá rovné sázky (červená/černá, sudá/lichá, vysoká/nízká čísla) a funguje následovně:
- Hráč si určí prvotní sázku a vsadí ji.
- Pokaždé když prohraje, zvýší vsazenou částku v následujícím kole o 1 díl. Pokaždé když vyhraje, vsazenou částku v následujícím kole o 1 díl sníží.
Řekněme, že si hráč zvolil 6$ prvotní sázku a začal hrát. Vsadí 6 $ a prohraje. Vsadí 7 $ a prohraje. Vsadí 8 $ a vyhraje. Vsadí 7 $ a prohraje. Vsadí 8 $ a vyhraje. Vsadí 7 $ a vyhraje. Celkově hráč vsadil šestkrát – třikrát vyhrál a třikrát prohrál. Přestože vyhrál i prohrál stejný počet sázek, je celkově tři dolary v plusu a na tom celá tato strategie stojí.
Když hráč používající D‘Alembertovu ruletovou strategii vyhraje i prohraje stejný počet kol, bude celkově v plusu o sumu, která odpovídá polovině odehraných kol. Pokud 10 kol vyhraje a zároveň 10 kol prohraje, bude bez ohledu na velikost prvotní sázky 10 $ v plusu.
Zpočátku to může znít dobře, protože k dosažení zisku vám stačí vyrovnat počet vyhraných a prohraných kol. Problém je v tom, že i když hrajete s tzv. rovnými sázkami, vaše šance na výhru nebo prohru nejsou 50:50 (navzdory jejich názvu). Ve skutečnosti na evropské ruletě statisticky vyhrajete pouze 48,65 % kol a zbylých 51,35 % kol prohrajete. Tento rozdíl stačí k tomu, aby D‘Alembertova strategie nebyla z dlouhodobého hlediska zisková.
Výhody a nevýhody D‘Alembertovy strategie
Výhodou tohoto systému vsázení je skutečnost, že je mnohem méně riskantní než strategie Martingale a Fibonacciho strategie. Určité riziko tu samozřejmě je, ale jelikož se sázky zvyšují během sérií proher pomalu, nepotřebujete tak velký rozpočet. Je mnohem méně pravděpodobné, že celý svůj rozpočet prohrajete a zároveň nejspíš nebudete mít problémy s maximálními a minimálními sázkami ruletového stolu.
Pomalé zvyšování velikosti sázek může být ale i nevýhodou. Mnoho peněz pomocí této strategie pravděpodobně nevyhrajete, alespoň ne když zohledníme prvotní sázku a počet kol, které musíte odehrát.
Navíc když vás potká série proher, zjistíte, že je velmi obtížné se vrátit do plusu. Potřebujete k tomu totiž podobně velkou sérii výher. Když to srovnáme s jinými strategiemi, tak u strategie Martingale potřebujete vyhrát pouze jedno kolo, abyste sérii proher zvrátili, a u Fibonacciho strategie je to sice více kol, ale ne tolik jako u D‘Alembertova systému.
Simulace D‘Alembertovy strategie
Při simulaci D‘Alembertovy strategie jsem si uvědomil, že nemůžu zvolit 1$ prvotní sázku, protože když hráči vyhrávají, sázky se mají zmenšovat. Kdyby byl prvotní sázkou 1 $, sázky by se neměly jak zmenšovat. Současně jsem nechtěl prvotní sázku příliš navyšovat, aby se daly výsledky jednotlivých strategií alespoň částečně porovnat.
Proto jsem se rozhodl u této strategie pro 5$ prvotní sázku a opět 1000$ rozpočet. Simulovaní hráči se řídili D‘Alembertovou strategií a když klesli na 1$ sázku, vsázeli dál 1 $, dokud neprohráli kolo a sázka se nezvýšila.
Toto jsou výsledky:
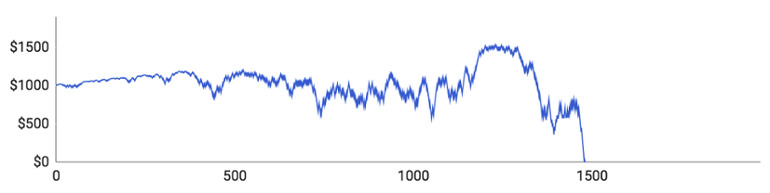
Pojďme se podívat na jednotlivé hráče:
- Hráč číslo 1 odehrál 1 480 kol, než vyčerpal všechny peníze. Rozpočet se mu podařilo navýšit maximálně o 532 $. Výše jeho sázek stále rostla, ale spolu s tím se prohlubovaly i vzestupy a propady. Maximální vsazená částka byla 58 $ a průměrně v každém kole vsadil 23,40 $.
- Hráči číslo 2 se dařilo nejvíce ze všech. Odehrál celkově 1 971 kol a rozpočet se mu podařilo navýšit maximálně o 824 $. Poté ho však potkal obrovský propad, který ho stáhl až na nulu. Jeho maximální vsazenou částkou bylo 62 $, ale protože se mu nadprůměrně dařilo, byla jeho průměrná sázka v každém kole pouze 16,75 $. Proto jeho sázky byly celkově velmi nízké.
- Hráč číslo 3 odehrál pouze 406 kol a příliš se mu nedařilo. Z celkových 406 kol vyhrál pouze 184 (45,3 %), což je mnohem horší než předpokládaných 48,65 %. Maximálně se mu podařilo navýšit rozpočet pouze o 56 $.
- Hráči číslo 4 se také moc nedařilo. Odehrál celkově 563 kol a jeho rozpočet dosáhl maxima ve výši 1 172 $. Jeho průměrná výše sázky byla 14,70 $ a maximální výše sázky 50 $.
- Hráč číslo 5 zažil podobnou zkušenost jako hráč číslo 3. Odehrál pouze 517 kol a jeho rozpočet nikdy nepřesáhl 1 086 $. Z celkových 517 kol jich vyhrál pouze 236 (45,7 %).
Možná jste si všimli, že jsem se u D‘Alembertovy strategie podrobněji zaměřil na velikost sázek a procento výher vůči prohrám. Je to dáno principem této strategie. Hráči budou totiž do plusu, pokud je počet vyhraných a prohraných kol stejný. Jenže tak to zkrátka v ruletě nefunguje.
Těchto 5 hráčů dohromady odehrálo 4 937 kol, ze kterých vyhráli 2 366 kol a 2 571 jich prohráli. To znamená, že celkově vyhráli pouze 47,9 % kol. Kvůli většímu počtu proher oproti výhrám velikost sázek obecně stále rostla, což mělo za následek i stále významnější vzestupy a propady.
Laboucherova ruletová strategie
Laboucherova ruletová strategie je komplikovanější než všechny ostatní strategie, které jsem v tomto článku zmínil. Musíte sledovat, kolik vsázíte, a sázky sčítat, což asi bude vyžadovat trochu praxe.
Laboucherova strategie funguje následovně:
- Hráč si vytvoří tzv. „sázkovou řadu", která mu určí výši prvotní sázky a do určité míry mu bude určovat i výši sázek v následujících kolech. Podoba sázkové řady závisí zcela na hráči. Může vypadat úplně jednoduše, například 1-1-1-1-1-1 nebo 1-2-3-4-5-6, nebo může být trochu složitější jako 1-2-4-4-3-7.
- Hráč potom vezme čísla z obou konců řady a sečte je dohromady. Jejich součet určí výši sázky v daném kole.
- Pokud prohraje, vezme součet těch dvou čísel, které právě vsadil, a dopíše ho na konec řady. Potom se vrátí k druhému kroku a pokračuje.
- Pokud vyhraje, tak čísla z obou konců řady přeškrtne. Potom se vrátí k druhému kroku a pokračuje.
- Pokud hráč všechna čísla v sázkové řadě vyškrtá, může začít od začátku, nebo si může vytvořit jinou sázkovou řadu.
Chápu, že to asi může znít příliš složitě, takže si to ještě vyjasníme na příkladu v níže uvedené tabulce.
| Kolo | Aktuální sázková řada | Vsazená částka | Výsledek kola |
|---|---|---|---|
| 1 | 1-2-3-4-5-6 | 1 + 6 = 7 | PROHRA |
| 2 | 1-2-3-4-5-6-7 | 1 + 7 = 8 | VÝHRA |
| 3 | 2-3-4-5-6 | 2 + 6 = 8 | PROHRA |
| 4 | 2-3-4-5-6-8 | 2 + 8 = 10 | PROHRA |
| 5 | 2-3-4-5-6-8-10 | 2 + 10 = 12 | VÝHRA |
| 6 | 3-4-5-6-8 | 3 + 8 = 11 | VÝHRA |
| 7 | 4-5-6 | 4 + 6 = 10 | ... |
U Laboucherovy strategie je vaším cílem zbavit se všech čísel v sázkové řadě. Když se vám to podaří, bude se váš zisk (bez ohledu na počet výher nebo proher) rovnat součtu čísel, se kterými jste začali.
Matematika, kterou se tato strategie řídí, funguje velmi dobře, ale nezapomínejte, že pravděpodobnost hraje ve prospěch kasina. To pochopitelně znamená, že vám tato strategie ruletu dlouhodobě porážet neumožní.
Výhody a nevýhody Laboucherovy strategie
Laboucherova strategie se s ohledem na rizikovost nachází někde mezi Fibonacciho a D‘Alembertovou strategií. Matematika na pozadí této strategie skutečně funguje, a pokud se vám podaří docílit minimálně stejného počtu prohraných a vyhraných kol, budete v plusu. Vy už však víte, že se to s největší pravděpodobností dlouhodobě dít nebude,
a pokud vás třeba postihne série proher, čísla ve vaší řadě začnou čím dál tím víc narůstat, vaše řada se bude stále prodlužovat a vy budete muset vsázet více a více peněz. A co je ještě horší, sázky se budou držet poměrně vysoko, i když začnete vyhrávat. K jejich významnějšímu snížení je pak zapotřebí dlouhá série výher.
Simulace Laboucherovy strategie
Simulace Laboucherovy strategie jsou docela složité, protože závisí na seznamu čísel, se kterými hráč začne. Pro níže uvedené simulace jsem se rozhodl použít tuto sázkovou řadu: 1-2-3-4-5-6.
Zde jsou grafy simulací:
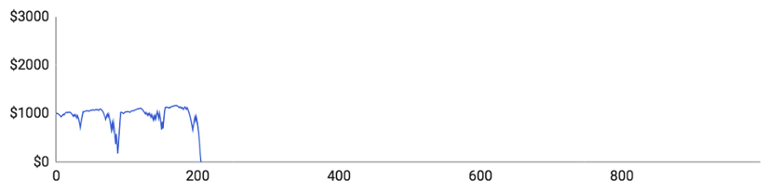
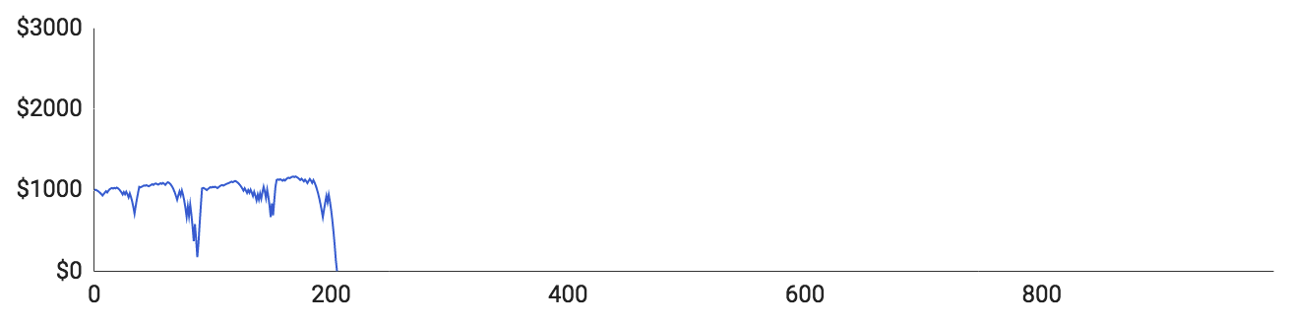
Jednotliví hráči dopadli následovně:
- Hráč číslo 1 odehrál 205 kol a jeho rozpočet dosahoval v maximu 1 170 $. Maximální výše sázky byla 240 $ a průměrná výše sázky 44,65 $. Potkal ho jeden obrovský propad, za kterého se mu podařilo dostat, ale při dalším propadu přišel o všechno.
- Hráč číslo 2 odehrál celkově 227 kol a jeho rozpočet dosáhl maxima ve výši 1 296 $. Jeho maximální sázka byla 272 $ a v průměru v každém kole vsázel 28,48 $.
- Hráč číslo 3 odehrál 350 kol a rozpočet se mu podařilo maximálně navýšit o 504 $. Jeho maximální sázka byla 377 $ a průměrná výše sázky dosáhla téměř 27 $. Jeho rozpočet narůstal poměrně stabilně, ale pak při jednom propadu přišel o všechno.
- Hráč číslo 4 měl velmi zajímavý průběh hry. Odehrál 996 kol, což je podstatně více, než čeho dosáhli ostatní hráči, a maximálně se mu podařilo rozpočet navýšit na 2 881 $. Vyhrál totiž 52,1 % kol, takže měl opravdu velké štěstí. Tato neuvěřitelná výherní úspěšnost mu ale nebyla nic platná, protože po obrovském propadu stejně skončil na nule.
- Hráč číslo 5 odehrál pouze 157 kol a rozpočet se mu podařilo v jednu chvíli navýšit o 201 $. Jeho maximální výše sázky byla 205 $ a průměrná výše sázky 31,57 $.
Výsledky této simulace jsou celkem zajímavé, zvlášť u hráče číslo 4, kterému se opravdu dařilo. Tyto příklady velmi dobře ukazují hlavní nevýhodu Laboucherovy strategie – rostoucí výši sázek způsobující ohromné vzestupy a propady.
Tato strategie (s počáteční sázkovou řadou 1-2-3-4-5-6) se zdá být nejriskantnější ze všech čtyř strategií uvedených v tomto článku. Rozpočty hráčů se poměrně rychle navyšovaly, ale zároveň hráči přišli o všechno v průměru nejrychleji. Pokud bych u této strategie zvolil jinou sázkovou řadu, mohl by být výsledek samozřejmě naprosto odlišný.
Lepší ruletové strategie
Jak jste si mohli všimnout, všechny strategie popsané v tomto článku jsou postavené na základech, které by zdánlivě měly fungovat, ale nakonec kvůli nim přijdete o celý svůj rozpočet. Proto vám nedoporučuji je používat.
Existují lepší strategie, které mohou maximalizovat vaše šance na opuštění kasina se ziskem nebo se alespoň postarají o to, že si při hraní užijete spoustu zábavy. Tím rozhodně neříkám, že s nimi budete dlouhodobě v plusu, ale když už budete nějaké strategie používat, vyzkoušejte tyto. Pokud se o nich chcete dozvědět více, přečtěte si můj článek o fungujících ruletových strategiích.